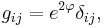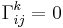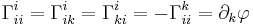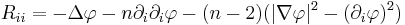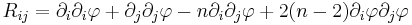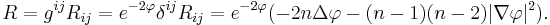List of formulas in Riemannian geometry
This is a list of formulas encountered in Riemannian geometry.
Contents |
Christoffel symbols, covariant derivative
In a smooth coordinate chart, the Christoffel symbols are given by:
Here 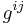 is the inverse matrix to the metric tensor
is the inverse matrix to the metric tensor 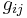 . In other words,
. In other words,
and thus
is the dimension of the manifold.
Christoffel symbols satisfy the symmetry relation
which is equivalent to the torsion-freeness of the Levi-Civita connection.
The contracting relations on the Christoffel symbols are given by
and
where |g| is the absolute value of the determinant of the metric tensor 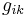 . These are useful when dealing with divergences and Laplacians (see below).
. These are useful when dealing with divergences and Laplacians (see below).
The covariant derivative of a vector field with components 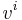 is given by:
is given by:
and similarly the covariant derivative of a 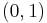 -tensor field with components
-tensor field with components 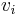 is given by:
is given by:
For a 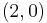 -tensor field with components
-tensor field with components 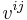 this becomes
this becomes
and likewise for tensors with more indices.
The covariant derivative of a function (scalar)  is just its usual differential:
is just its usual differential:
Because the Levi-Civita connection is metric-compatible, the covariant derivatives of metrics vanish,
The geodesic 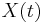 starting at the origin with initial speed
starting at the origin with initial speed 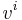 has Taylor expansion in the chart:
has Taylor expansion in the chart:
Curvature tensors
Riemann curvature tensor
If one defines the curvature operator as ![R(U,V)W=\nabla_U \nabla_V W - \nabla_V \nabla_U W -\nabla_{[U,V]}W](/2012-wikipedia_en_all_nopic_01_2012/I/afd19f70d73e2f9ccd4957db1cf961cd.png) and the coordinate components of the
and the coordinate components of the 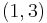 -Riemann curvature tensor by
-Riemann curvature tensor by 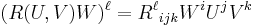 , then these components are given by:
, then these components are given by:
where n denotes the dimension of the manifold. Lowering indices with 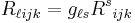 one gets
one gets
The symmetries of the tensor are
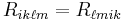 and
and 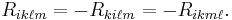
That is, it is symmetric in the exchange of the first and last pair of indices, and antisymmetric in the flipping of a pair.
The cyclic permutation sum (sometimes called first Bianchi identity) is
The (second) Bianchi identity is
that is,
which amounts to a cyclic permutation sum of the last three indices, leaving the first two fixed.
Ricci and scalar curvatures
Ricci and scalar curvatures are contractions of the Riemann tensor. They simplify the Riemann tensor, but contain less information.
The Ricci curvature tensor is essentially the unique nontrivial way of contracting the Riemann tensor:
The Ricci tensor 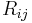 is symmetric.
is symmetric.
By the contracting relations on the Christoffel symbols, we have
The scalar curvature is the trace of the Ricci curvature,
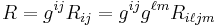 .
.
The "gradient" of the scalar curvature follows from the Bianchi identity (proof):
that is,
Einstein tensor
The Einstein tensor Gab is defined in terms of the Ricci tensor Rab and the Ricci scalar R,
where g is the metric tensor.
The Einstein tensor is symmetric, with a vanishing divergence (proof) which is due to the Bianchi identity:
Weyl tensor
The Weyl tensor is given by
where  denotes the dimension of the Riemannian manifold.
denotes the dimension of the Riemannian manifold.
Gradient, divergence, Laplace–Beltrami operator
The gradient of a function  is obtained by raising the index of the differential
is obtained by raising the index of the differential 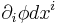 , that is:
, that is:
The divergence of a vector field with components 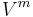 is
is
The Laplace–Beltrami operator acting on a function  is given by the divergence of the gradient:
is given by the divergence of the gradient:
The divergence of an antisymmetric tensor field of type 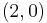 simplifies to
simplifies to
Kulkarni–Nomizu product
The Kulkarni–Nomizu product is an important tool for constructing new tensors from existing tensors on a Riemannian manifold. Let  and
and  be symmetric covariant 2-tensors. In coordinates,
be symmetric covariant 2-tensors. In coordinates,
Then we can multiply these in a sense to get a new covariant 4-tensor, which we denote  . The defining formula is
. The defining formula is
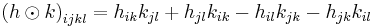
Often the Kulkarni–Nomizu product is denoted by a circle with a wedge that points up inside it. However, we will use  instead throughout this article. Clearly, the product satisfies
instead throughout this article. Clearly, the product satisfies
Let us use the Kulkarni–Nomizu product to define some curvature quantities.
Weyl tensor
The Weyl tensor 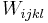 is defined by the formula
is defined by the formula
Each of the summands on the righthand side have remarkable properties. Recall the first (algebraic) Bianchi identity that a tensor 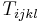 can satisfy:
can satisfy:
Not only the Riemann curvature tensor on the left, but also the three summands on the right satisfy this Bianchi identity. Furthermore, the first factor in the second summand has trace zero. The Weyl tensor is a symmetric product of alternating 2-forms,
just like the Riemann tensor. Moreover, taking the trace over any two indices gives zero,
In fact, any tensor that satisfies the first Bianchi identity can be written as a sum of three terms. The first, a scalar multiple of  . The second, as
. The second, as 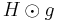 where
where  is a symmetric trace-free 2-tensor. The third, a symmetric product of alternating two-forms which is totally traceless, like the Weyl tensor described above.
is a symmetric trace-free 2-tensor. The third, a symmetric product of alternating two-forms which is totally traceless, like the Weyl tensor described above.
The most remarkable property of the Weyl tensor, though, is that it vanishes (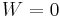 )if and only if a manifold
)if and only if a manifold  of dimension
of dimension 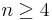 is locally conformally flat. In other words,
is locally conformally flat. In other words,  can be covered by coordinate systems in which the metric
can be covered by coordinate systems in which the metric 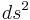 satisfies
satisfies
This is essentially because 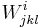 is invariant under conformal changes.
is invariant under conformal changes.
In an inertial frame
An orthonormal inertial frame is a coordinate chart such that, at the origin, one has the relations 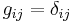 and
and 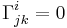 (but these may not hold at other points in the frame). In such a frame, the expression for several operators is simpler. Note that the formulae given below are valid at the origin of the frame only.
(but these may not hold at other points in the frame). In such a frame, the expression for several operators is simpler. Note that the formulae given below are valid at the origin of the frame only.
Under a conformal change
Let  be a Riemannian metric on a smooth manifold
be a Riemannian metric on a smooth manifold  , and
, and  a smooth real-valued function on
a smooth real-valued function on  . Then
. Then
is also a Riemannian metric on  . We say that
. We say that 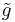 is conformal to
is conformal to  . Evidently, conformality of metrics is an equivalence relation. Here are some formulas for conformal changes in tensors associated with the metric. (Quantities marked with a tilde will be associated with
. Evidently, conformality of metrics is an equivalence relation. Here are some formulas for conformal changes in tensors associated with the metric. (Quantities marked with a tilde will be associated with 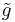 , while those unmarked with such will be associated with
, while those unmarked with such will be associated with  .)
.)
Note that the difference between the Christoffel symbols of two different metrics always form the components of a tensor.
Here 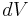 is the Riemannian volume element.
is the Riemannian volume element.
Here  is the Kulkarni-Nomizu product defined earlier in this article. The symbol
is the Kulkarni-Nomizu product defined earlier in this article. The symbol 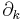 denotes partial derivative, while
denotes partial derivative, while 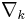 denotes covariant derivative.
denotes covariant derivative.
Beware that here the Laplacian  is minus the trace of the Hessian on functions,
is minus the trace of the Hessian on functions,
Thus the operator 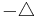 is elliptic because the metric
is elliptic because the metric  is Riemannian.
is Riemannian.
If the dimension 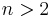 , then this simplifies to
, then this simplifies to
We see that the (3,1) Weyl tensor is invariant under conformal changes.
Let  be a differential
be a differential  -form. Let
-form. Let  be the Hodge star, and
be the Hodge star, and  the codifferential. Under a conformal change, these satisfy
the codifferential. Under a conformal change, these satisfy
Conformally flat manifolds
WARNING: THE FORMULAS BELOW ARE UNCHECKED AND COULD VERY WELL BE WRONG
The setting where the metric takes the form
where 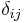 is the standard Euclidean metric, is particularly simple. These manifolds are called conformally flat. In what follows, all the partial derivatives
is the standard Euclidean metric, is particularly simple. These manifolds are called conformally flat. In what follows, all the partial derivatives 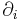 and the Laplacian
and the Laplacian  are with respect to the Euclidean metric.
are with respect to the Euclidean metric.
The Christoffel symbols are
for  ,
,  , and
, and  all distinct.
all distinct.
In this setting, the Ricci tensor takes the form
for  and
and  distinct. The scalar curvature thus is
distinct. The scalar curvature thus is
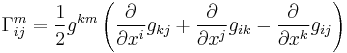
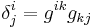
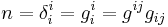
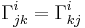
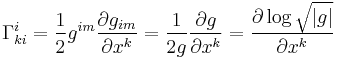
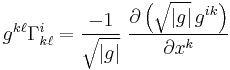
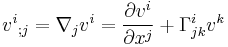
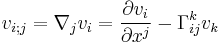
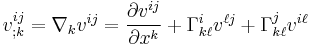
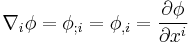
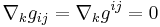
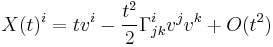
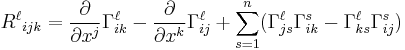
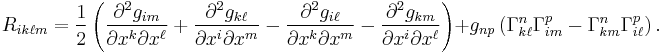
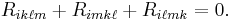
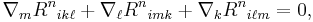
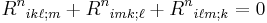
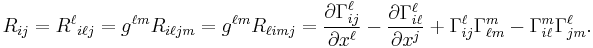
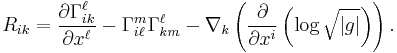
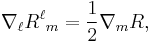
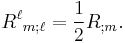
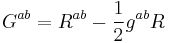
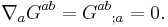
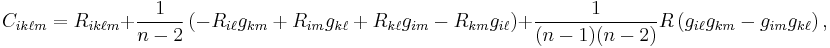
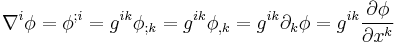
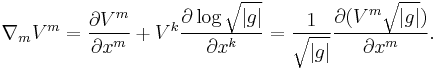
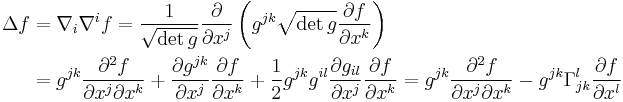
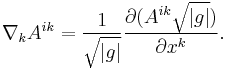

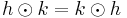
![R_{ijkl} = -\frac{R}{2n(n-1)}(g\odot g)_{ijkl} %2B \frac{1}{n-2}\left[ \left(Ric -\frac{R}{n}g\right) \odot g \right]_{ijkl} %2B W_{ijkl}](/2012-wikipedia_en_all_nopic_01_2012/I/304f6b8f190f4fd8d3dd64a8e77fa83f.png)
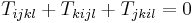

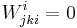
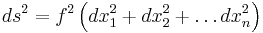
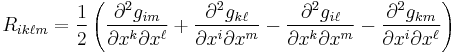
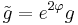
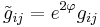
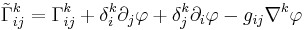
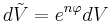
![\tilde R_{ijkl} = e^{2\varphi}\left( R_{ijkl} - \left[ g \odot \left( \nabla\partial\varphi - \partial\varphi\partial\varphi %2B \frac{1}{2}\|\nabla\varphi\|^2g \right)\right]_{ijkl} \right)](/2012-wikipedia_en_all_nopic_01_2012/I/c5fab2096a890c4e6986e73bb2ec2019.png)
![\tilde R_{ij} = R_{ij} - (n-2)\left[ \nabla_i\partial_j \varphi - (\partial_i \varphi)(\partial_j \varphi) \right] %2B \left( \triangle \varphi - (n-2)\|\nabla \varphi\|^2 \right)g_{ij}](/2012-wikipedia_en_all_nopic_01_2012/I/667ef988dd8b776aecb1ac9989d8b876.png)
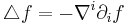
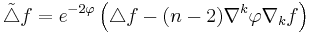
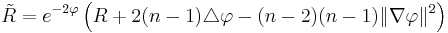
![\tilde R = e^{-2\varphi}\left[R %2B \frac{4(n-1)}{(n-2)}e^{-(n-2)\varphi/2}\triangle\left( e^{(n-2)\varphi/2} \right) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/208505f0b38e8b724d0a71d0de55e156.png)
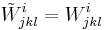
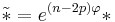
 = e^{-2\varphi}\left[ \delta\omega - (n-2p)\omega\left(\nabla\varphi, v_1, v_2, \ldots , v_{p-1}\right) \right]](/2012-wikipedia_en_all_nopic_01_2012/I/f157fd4b58d7f3e74421868809132abc.png)